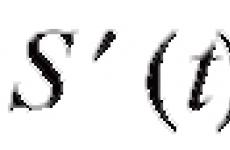Способы вычисления интегралов. II. Основные методы интегрирования. Интегралы от дифференциальных биномов
Определение . Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции (или подынтегрального выражения) и применяя свойства неопределенного интеграла приводится к одному или нескольким табличным интегралам называется непосредственным интегрированием .
Часто при непосредственном интегрировании используются следующие преобразования дифференциала (операция «внесения под знак дифференциала»):
Например . 1) ;
При вычислении данных интегралов пользовались формулами 1 и 2 таблицы интегралов, которая приведена ниже.
Таблица основных неопределенных интегралов.
- Метод интегрирования подстановкой (заменой переменной).
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования. При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся.
Данный метод интегрирования основывается на следующей теореме:
Теорема. Пусть функцию f(x) можно представить в виде: f(x)=g(j(x))×j¢(х), тогда если G(u) является первообразной для g(u), то и G(j(x)) является первообразной для g(j(x)). То есть имеет место равенство: .
Например.
- Метод интегрирования по частям.
Интегрирование по частям состоит в том, что подынтегральное выражение некоторого интеграла представляется в виде произведения двух сомножителей u и dv, затем используется формула интегрирования по частям.
Теорема Пусть функции u(x) и v(x) дифференцируемы, тогда имеет место формула:
Так как u¢(x)dx=du, v¢(x)dx=dv, то формулу можно переписать в виде:
Например.
Формулу интегрирования по частям в процессе решения можно применять несколько раз.
Например
Например
перенесем из правой части равенства в левую:
Некоторые типы интегралов, которые удобно вычислять методом интегрирования по частям:
| ; ; , где Р(х)– многочлен от х, к – некоторое число | u=P(x), dv – остальные множители |
| ; ; ; ; | dv=P(x)dх, u – все остальные множители |
| ; , где а и b – некоторые числа | , dv – остальные множители |
- Интегрирование рациональных дробей.
ОпределениеРациональными будем называть дроби вида , где P n (x), Q m (x) многочлены соответственно n-ой и m-ой степени от х. К простейшим рациональным дробям отнесем дроби четырех типов:
Где А и а – некоторые действительные числа, – простейшая дробь первого типа;
– простейшая дробь второго типа;
– простейшая дробь третьего типа;
– простейшая дробь четвертого типа.
Рассмотрим интегрирование дробей первых трех типов.
3) Интегрирование простейшей дроби третьего типа проводится в два этапа. Разберем процесс интегрирования на примере.
(выделим в числителе производную знаменателя для последующего внесения под знак дифференциала: (х 2 +2х+3)¢=2х+2)
Определение Рациональные дроби называются правильными если степень многочлена в числителе меньше степени многочлена в знаменателе и неправильными если степень многочлена в числителе больше или равна степени многочлена в знаменателе.
В случае неправильной рациональной дроби возможно выделить целую часть. Для этого многочлен из числителя делят с остатком на многочлен знаменателя. Полученное частное будет целой частью, а остаток – числителем новой правильной рациональной дроби. Например, выделим целую часть: .
Таким образом, интегрирование рациональных дробей в обоих случаях сводится к интегрированию правильной рациональной дроби, которая не всегда является простейшей рациональной дробью одного из четырех типов.
Рассмотрим некоторый многочлен Q(x). Пусть число а является корнем этого многочлена, тогда Q(x)=(х-а)Q 1 (x), где Q 1 (x) – многочлен степени на 1 меньше степени Q(x). Число а может быть корнем кратности к, тогда Q(x)=(х-а) к Q 2 (x), где Q 2 (x) – многочлен степени на к меньше степени Q(x). Кроме того, многочлен Q(x) наряду с действительными корнями может иметь комплексный корень a+bi, тогда комплексное число a-bi также будет корнем Q(x). В этом случае Q(x)=(х 2 +px+q)Q 3 (x), где х 2 +px+q=(х-(a+bi))(х-(a-bi)). Если же указанные комплексные числа являются корнями кратности m, тогда Q(x)=(х 2 +px+q) m Q 4 (x).
Таким образом, всякий многочлен Q(x) можно представить в виде:
Q(x)=(х-а 1) к 1 (х-а 2) к 2 …(х-а n) k n (х 2 +p 1 x+q 1) m 1 (х 2 +p 2 x+q 2) m 2 …(х 2 +p s x+q s) m s .
Теорема. Любую правильную рациональную дробь можно представить в виде суммы простейших рациональных дробей 1-4 типов.
Например. Рассмотрим алгоритм представления правильной рациональной дроби в виде суммы простейших рациональных дробей 1-4 типов.
Так как знаменатели дробей равны, очевидно, должны быть равны и числители, а это равенство возможно при равенстве коэффициентов при одинаковых степенях х. Таким образом, подставив вместо неопределенных коэффициентов A, B, C их значения получим: .
Например Найти интеграл .
Подынтегральная функция является неправильной рациональной дробью. После деления числителя на знаменатель с остатком получим: .
Разложим правильную рациональную дробь на простейшие методом неопределенных коэффициентов:
Отсюда следует, что Решая полученную систему линейных уравнений, получаем Тогда , то есть = ;
Найдем отдельно
Таким образом, .
- Интегрирование тригонометрических функций.
1. Пусть необходимо найти , где R – некоторая функция
При отыскании таких интегралов часто бывает полезно воспользоваться универсальной тригонометрической подстановкой: . С ее помощью всегда можно перейти от интеграла тригонометрической функции к интегралу от рациональной функции:
Х=2arctgt, .
2. Если функция R(sinx, cosx) нечетна относительно sinx, то есть R(-sinx, cosx)=- R(sinx, cosx), то применяют подстановку cosx=t;
3. Если функция R(sinx, cosx) нечетна относительно соsx, то есть R(sinx, -cosx)=- R(sinx, cosx), то применяют подстановку sinx=t;
4. Если функция R(sinx, cosx) четна относительно sinx и соsx, то есть R(-sinx, -cosx)=R(sinx, cosx), то применяют подстановку tgx=t; такая же подстановка применяется в случае .
Например.
Например Найти интеграл . Подынтегральная функция четна относительно sinx, тогда применяем подстановку tgx=t.
5. Для нахождения интегралов вида используют следующие приемы:
а) если n – нечетное целое положительное число, то используют подстановку sinx=t;
б) если m – нечетное целое положительное число, то используют подстановку соsx=t;
в) если m и n – целые неотрицательные четные числа, то используют формулы понижения порядка ; ; ;
г) если m+n – четное отрицательное целое число, то используют подстановку tgx=t.
Например. .
Например. . ; приводятся к интегралам от тригонометрических функций с помощью следующих подстановок:
а) для интеграла подстановка х=a×sint;
б) для интеграла подстановка х=a×tgt;
в) для интеграла подстановка .
Лекция 12
1 . Непосредственное интегрирование – вычисление интегралов с помощью таблицы простейших интегралов, правил интегрирования и свойств неопределенных интегралов.
Пример 1 . +С .
Использована формула тригонометрии: .
Пример2 .
здесь выполнено очевидное преобразование подынтегрального выражения, и вместо переменной интегрирования х принято выражение (a–bx ), относительно этой переменной получается табличный интеграл. Такой прием иногда называют «загонкой » под знак дифференциала некоторого выражения.
Действительно: .
2 . Метод замены переменной . Метод подстановки .
Пусть y =f(x), x X . Введем новую переменную t , положив x =(t) , t T , тогдаy =f(x) =f((t)) ; dx =(t)dt и
После интегрирования последнего выражения нужно в результате перейти к старой переменной.
Этот метод применяется, когда подынтегральная функция является сложной функцией.
Пример. Найти интеграл: .
Решение .
1. Замена переменной : х=t/4 , тогда dx=dt/4.
Подставив х и dx в исходный интеграл, получим:
= .
2. Подстановка : 4х = t , тогда dx = dt/4 . Получим тот же ответ.
3. Метод интегрирования « по частям» .
Пусть в промежутке Х заданы две непрерывно дифференцируемые функции u(x) и v(x) .
Запишем выражение для дифференциала их произведения:
Проинтегрируем левую и правую части полученного выражения:
отсюда следует формула интегрирования по частям:
Метод интегрирования по частям применяют для целого класса интегралов, например, когда подынтегральная функция содержит:
1) какую-либо функцию, которой нет в таблице простейших интегралов:
или ее произведение на многочленP(x) :
, .
В этом случае за u принимают, соответственно, , и т. д., а за dv – выражение P (x )dx ., так что одна из первообразных v легко может быть определена: ,
(здесь при интегрировании произвольную постоянную следует опустить);
2) произведение многочлена на тригонометрическую функцию или на экспоненту: .
В этом случае за u следует принять P(x) , а за dv – остальную часть подынтегрального выражения: exdx, sin xdx, и т.д.
Операцию интегрирования по частям можно применять многократно, что иногда позволяет решить задачу.
Пример 1 . Найти интеграл .
Решение .
Положим ln x = u , dx = dv (здесь P (x ) =1 ).
Тогда du = d (ln x ) = , v = = x – одна из первообразных.
Используя формулу интегрирования по частям ,
получаем:
= xln x – =x ln x – = x ln x – x + C = x (ln x – 1 ) + C .
Пример 2 .
Найти интеграл .
Решение.
Пусть x =u (P(x) =x ), =dvdu = , v =.
Используя формулу интегрирования по частям, получаем:
= x sin x – = x sin x + cos x + C .
Пример 3 . Найти интеграл .
Решение .
Положим x =u , e x dx =dv .
Тогда du = dx , v =ex .
=xe x –=xe x – e x = e x (x – 1 ) +С.
Пример 4 . Найти интеграл .
Решение .
Положим x 2 =u , e х dx =dv .
Тогда du =2xdx , v =e x .
По формуле интегрирования по частям получаем:
=x 2 ∙e x –2 .
Применим еще раз интегрирование по частям (см. пример 3):
x 2 e x –2 = x 2 e x – 2(xe x – e x) + C =
= e x (х 2 –2x +2) +C .
4. Метод неопределенных коэффициентов
Применяется для интегрирования рациональных функций
где и – многочлены, и степень числителя меньше степени знаменателя (правильная дробь), неправильную дробь можно путем деления многочлена на многочлен свести к сумме некоторого многочлена и правильной дроби.
По теореме из алгебры, всякий многочлен степени n со старшим коэффициентом, равным единице, имеющий действительные различные корни x 1 , x 2 , ..., x n , можно представить так:
Q (x )=( x – x 1 )(x – x 2 )(x – x n ).
Тогда правильную дробь можно разложить на простейшие дроби и записать:
где A 1 , A 2 , ..., A n – некоторые числа (неопределенные коэффициенты).
Приведя правую часть выражения к общему знаменателю и приравняв затем коэффициенты при одинаковых степенях х в числителе левой и правой части, получим систему уравнений для определения неизвестных коэффициентов A 1 , A 2 , ...,A n .
После этого интегрирование рациональной функции сводится к нахождению n интегралов вида:
Пример . Найти интеграл .
Решение. Подынтегральная функция есть правильная дробь, разложим ее на простейшие дроби.
Знаменатель имеет вещественные, различные корни: x 1 = 0 , x 2 =2 , x 3 = –2 . Следовательно, x3–4x = x (x–2 )(x +2 ) ,
4.1. ПРОСТЕЙШИЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ 4.1.1. Понятие неопределенного интеграла
В дифференциальном исчислении рассматривалась задача нахождения производной или дифференциала по заданной функции y = F(x), т. е. необходимо было найти f (x) = F"(x) или dF(x) = F"(x) dx = f (x) dx. Поставим обратную задачу: восстановить продифференцированную функцию, т. е., зная производную f(x) (или дифференциал f(x)dx), найти такую функцию F(x), чтобы F"(x) = f (x). Эта задача оказывается значительно более трудной, чем задача дифференцирования. Например, пусть известна скорость перемещения точки, а надо найти закон
ее перемещения S
= S(t),
причем Для решения подобных
Для решения подобных
задач вводятся новые понятия и действия.
Определение. Дифференцируемая функция F(x) называется первообразной для функции f (x) на (a; b), если F"(x) = f (x) на (a; b).
Например, для f
(x) = x 2 первообразная  так как
так как
 для f
(x) = cos x
первообразной будет F(x) = sin x, потому что F"(x) = (sin x)" = cos x, что совпадает с f
(x).
для f
(x) = cos x
первообразной будет F(x) = sin x, потому что F"(x) = (sin x)" = cos x, что совпадает с f
(x).
Всегда ли существует первообразная для заданной функции f (x)? Да, если эта функция непрерывна на (a; b). Кроме того, первообразных бесчисленное множество, и отличаются они друг от друга только постоянным слагаемым. Действительно, sin x + 2, sin x - 2, sin x + c - все эти функции будут первообразными для cos x (производная от постоянной величины равна 0) - рис. 4.1.
Определение.
Выражение F(x)
+ C,
где С
- произвольная постоянная величина, определяющее множество первообразных для функции f (x),
называется неопределенным интегралом
и обозначается символом  , т. е.
, т. е. , где знак - знак неопределенного
, где знак - знак неопределенного
интеграла, f (x) - называется подынтегральной функцией, f (x)dx - подынтегральньм выражением, х - переменной интегрирования.

Рис. 4.1. Пример семейства интегральных кривых
Определение. Операция нахождения первообразной по заданной производной или дифференциалу называется интегрированием этой функции.
Интегрирование - действие, обратное дифференцированию, его можно проверить дифференцированием, причем дифференцирование однозначно, а интегрирование дает ответ с точностью до постоянной. Придавая постоянной величине С
конкретные значения по-
по-
лучим различные функции
каждая из которых задает на координатной плоскости кривую, называемую интегральной. Все графики интегральных кривых сдвинуты параллельно относительно друг друга вдоль оси Oy. Следовательно, геометрически неопределенный интеграл представляет собой семейство интегральных кривых.
Итак, введены новые понятия (первообразной и неопределенного интеграла) и новое действие (интегрирование), но как все-таки находить первообразную? Чтобы легко было ответить на этот вопрос, надо в первую очередь составить и выучить наизусть таблицу неопределенных интегралов от основных элементарных функций. Она получается в результате обращения соответствующих формул дифференцирования. Например, если
Обычно в таблицу включаются некоторые интегралы, полученные после применения простейших методов интегрирования. Эти формулы помечены в табл. 4.1 символом «*» и доказаны при дальнейшем изложении материала.
Таблица 4.1. Таблица основных неопределенных интегралов

Формула 11 из табл. 4.1 может иметь вид ,
,
так как. Аналогичное замечание и по поводу фор-
мулы 13:

4.1.2. Свойства неопределенных интегралов
Рассмотрим простейшие свойства неопределенного интеграла, которые позволят интегрировать не только основные элементарные функции.
1.Производная от неопределенного интеграла равна подынтегральной функции:
2.Дифференциал от неопределенного интеграла равен подынтегральному выражению:
3.Неопределенный интеграл от дифференциала функции равен этой функции, сложенной с произвольной постоянной:
Пример 1. Пример 2.
Пример 2.
4.Постоянный множитель можно выносить за знак интеграла: Пример 3.
5.Интеграл от суммы или разности двух функций равен сумме или разности интегралов от этих функций:
Пример 4.
Формула интегрирования остается справедливой, если переменная интегрирования является функцией: если  то
то
Произвольная функция, имеющая непрерывную производную. Это свойство называется инвариантностью.
Пример 5. , поэтому
, поэтому
Сравнить с
Универсального способа интегрирования не существует. Далее будут приведены некоторые методы, позволяющие вычислить заданный интеграл с помощью свойств 1-5 и табл. 4.1.
4.1.3.Непосредственное интегрирование
Этот метод заключается в прямом использовании табличных интегралов и свойств 4 и 5. Примеры.

4.1.4.Метод разложения
Этот метод заключается в разложении подынтегральной функции в линейную комбинацию функций с уже известными интегралами.
Примеры.

4.1.5. Метод подведения под знак дифференциала
Для приведения данного интеграла к табличному бывает удобно сделать преобразования дифференциала.
1. Подведение под знак дифференциала линейной функции
 отсюда
отсюда в частности, dx =
d(x
+
b),
в частности, dx =
d(x
+
b),
 дифференциал не меняется, если к переменной прибавить
дифференциал не меняется, если к переменной прибавить
или отнять постоянную величину. Если переменная увеличивается в несколько раз, то дифференциал умножается на обратную величину. Примеры с решениями.


Проверим формулы 9*, 12* и 14* из табл. 4.1, используя метод подведения под знак дифференциала:

что и требовалось доказать.
2. Подведение под знак дифференциала основных элементарных функций:



Замечание. Формулы 15* и 16* могут быть проверены дифференцированием (см. свойство 1). Например,

а это и есть подынтегральная функция из формулы 16*.
4.1.6. Метод выделения полного квадрата из квадратичного трехчлена
При интегрировании выражений типа  или
или
 выделением полного квадрата из квадратного трехчлена
выделением полного квадрата из квадратного трехчлена
ax 2 + bx + c удается свести их к табличным 12*, 14*, 15* или 16* (см. табл. 4.1).
Поскольку в общем виде эта операция выглядит сложнее, чем на самом деле, ограничимся примерами.
Примеры.
1.
Решение. Здесь мы выделяем полный квадрат из квадратного трехчлена x 2 + 6x + 9 = (x 2 + 6x + 9) - 9 + 5 = (x + 3) 2 - 4 , а затем используем метод подведения под знак дифференциала.
Рассуждая аналогично, можно вычислить следующие интегралы:
2. 3.

На заключительном этапе интегрирования была использована формула 16*.
4.1.7. Основные методы интегрирования
Таких методов два: метод замены переменной, или подстановка, и интегрирование по частям.
Метод замены переменной
Существуют две формулы замены переменной в неопределенном интеграле:
1) 2)
Здесьсуть монотонные дифференцируемые функ-
ции своих переменных.
Искусство применения метода состоит, в основном, в выборе функцийтак, чтобы новые интегралы являлись табличными или сводились к ним. В окончательном ответе следует вернуться к старой переменной.
Заметим, что подведение под знак дифференциала является частным случаем замены переменной.
Примеры.

Решение. Здесь следует ввести новую переменную t так, чтобы избавиться от квадратного корня. Положим x + 1 = t, тогда x = t 2 + 1, а dx = 2 tdt:

Решение. Заменив x - 2 на t, получим в знаменателе одночлен и после почленного деления интеграл сведется к табличному от степенной функции:



При переходе к переменной x использованы формулы:
Метод интегрирования по частям
Дифференциал произведения двух функций определяется формулой
Интегрируя это равенство (см. свойство 3), найдем:

Отсюда Это и есть формула интегрирования по
Это и есть формула интегрирования по
частям.
Интегрирование по частям предполагает субъективное представление подынтегрального выражения в виде u
. dV,
и при этом интеграл  должен быть проще, чем
должен быть проще, чем В противном случае применение
В противном случае применение
метода не имеет смысла.
Итак, метод интегрирования по частям предполагает умение выделять из подынтегрального выражения сомножители u и dV с учетом вышеизложенных требований.
Приведем ряд типичных интегралов, которые могут быть найдены методом интегрирования по частям. 1. Интегралы вида
где P(x) - многочлен; k - постоянная. В этом случае u = P(x), а dV - все остальные сомножители.
Пример 1.

2.Интегралы типа
Здесь положим- другие сомножители.
Пример 2.

Пример 3.  Пример 4.
Пример 4.

Любой результат можно проверить дифференцированием. Напр мер, в данном случае
Результат верен.
3.Интегралы вида
где a, b - const. За u следует взять e ax , sin bx или cos bx.
Пример 5.

Отсюда получаем Пример 6.

Отсюда

Пример 7.  Пример 8.
Пример 8.
Решение. Здесь надо сперва сделать замену переменной, а потом интегрировать по частям:
Пример 9.  Пример 10.
Пример 10.
Решение. Этот интеграл с равным успехом может быть найден как в результате замены переменной 1 + х 2 = t 2 , так и методом интегрирования по частям:

Самостоятельная работа
Выполнить непосредственное интегрирование (1-10).

Применить простейшие методы интегрирования (11-46).



Выполнить интегрирование, используя методы замены переменной и интегрирования по частям (47-74).



Под непосредственным интегрированием понимают такой способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам.
Пример 1. Найти.
Разделив числитель на знаменатель, получим:
= .
.
Отметим, что нет надобности после каждого слагаемого ставить произвольную постоянную, потому что их сумма есть также произвольная постоянная, которую мы пишем в конце.
Пример 2.
Найти .
.
Преобразуем подынтегральную функцию следующим образом:
 .
.
Применив табличный интеграл 1, получим:
 .
.
Пример 3.
Пример 4.
Пример 5.
= .
.
В некоторых случаях нахождение интегралов упрощается применением искусственных приемов.
Пример 6.
Найти .
.
Умножив подынтегральное выражение
на
 находим
находим
= .
.
Пример 7 .
Пример 8 .
2. Интегрирование методом замены переменной
Вычислить заданный интеграл непосредственным интегрированием удается далеко не всегда, а иногда это связано с большими трудностями. В этих случаях применяют другие приемы. Одним из наиболее эффективных является метод замены переменной. Сущность его заключается в том, что путем введения новой переменной интегрирования удается свести заданный интеграл к новому, который сравнительно легко берется непосредственно. Существуют два варианта этого метода.
а) Метод подведения функции под знак дифференциала
По определению дифференциала функции
 .
.
Переход в этом равенстве слева направо
называют "подведением множителя
 под
знак дифференциала".
под
знак дифференциала".
Теорема об инвариантности формул интегрирования
Всякая формула интегрирования сохраняет свой вид при подстановке вместо независимой переменной любой дифференцируемой функции от нее, т.е., если
 , то и
, то и ,
,
где
 - любая дифференцируемая функция отx
.
Ее значения должны принадлежать
интервалу, в котором функция
- любая дифференцируемая функция отx
.
Ее значения должны принадлежать
интервалу, в котором функция определена и непрерывна.
определена и непрерывна.
Доказательство:
Из того, что
 ,
следует
,
следует .
Возьмем теперь функцию
.
Возьмем теперь функцию .
Для ее дифференциала в силу свойства
инвариантности формы первого дифференциала
функции имеем
.
Для ее дифференциала в силу свойства
инвариантности формы первого дифференциала
функции имеем
Пусть требуется вычислить интеграл
 .
Предположим, что существуют дифференцируемая
функция
.
Предположим, что существуют дифференцируемая
функция и функция
и функция такие, что подынтегральное выражение
такие, что подынтегральное выражение
 может быть записано в виде
может быть записано в виде
т.е.
вычисление интеграла
 сводится к вычислению интеграла
сводится к вычислению интеграла и последующей подстановке
и последующей подстановке .
.
Пример 1. .
Пример 2. .
Пример 3 . .
Пример 4 . .
Пример
5
.
 .
.
Пример 6 . .
Пример 7 . .
Пример 8. .
Пример 9. .
Пример 10 . .
Пример 11.
Пример
12
.
НайтиI= (0).
(0).
Представим подынтегральную функцию в виде:
Следовательно,
Таким образом,
 .
.
Пример
12а.
НайтиI
= ,
,
 .
.
Так как
 ,
,
следовательно I = .
Пример 13.
Найти (0).
(0).
Для
того, чтобы свести этот интеграл к
табличному, разделим числитель и
знаменатель подынтегрального выражения
на
 :
:
 .
.
Мы подвели постоянный множитель под знак дифференциала. Рассматриваякак новую переменную, получим:
 .
.
Вычислим также интеграл, который имеет важное значение при интегрировании иррациональных функций.
Пример
14.
НайтиI= (х
а
,а
0).
(х
а
,а
0).
Имеем
 .
.
Итак,

 (х
а
,а
0).
(х
а
,а
0).
Представленные примеры иллюстрируют важность умения приводить данное
дифференциальное
выражение
 к виду
к виду ,
где
,
где есть некоторая функция отx
иg
– функция более простая для интегрирования,
чемf
.
есть некоторая функция отx
иg
– функция более простая для интегрирования,
чемf
.
В этих примерах были проведены преобразования дифференциала, такие как


 гдеb
– постоянная
величина
гдеb
– постоянная
величина


 ,
,
 ,
,
 ,
,
часто используемые при нахождении интегралов.
В таблице основных интегралов предполагалось, что x есть независимая переменная. Однако, эта таблица, как следует из изложенного выше, полностью сохраняет свое значение, если подx понимать любую непрерывно дифференцируемую функцию от независимой переменной. Обобщим ряд формул таблицы основных интегралов.
3а.
 .
.
4.
 .
.
5.
 =
= .
.
6.

 =
=
 .
.
7.
 =
=
 .
.
8.
 (х
а
,а
0).
(х
а
,а
0).
9.
 (а
0).
(а
0).
Операция подведения функции
 под знак дифференциала эквивалентна
замене переменнойх
на новую переменную
под знак дифференциала эквивалентна
замене переменнойх
на новую переменную .
Нижеследующие примеры иллюстрируют
это положение.
.
Нижеследующие примеры иллюстрируют
это положение.
Пример
15.
НайтиI= .
.
Произведем замену переменной по формуле
 ,
тогда
,
тогда ,
т.е.
,
т.е. иI=
иI= .
.
Заменив u
его выражением ,
окончательно получим
,
окончательно получим
I= .
.
Выполненное преобразование эквивалентно
подведению под знак дифференциала
функции
 .
.
Пример 16.
Найти .
.
Положим
 ,
тогда
,
тогда ,
откуда
,
откуда .
Следовательно,
.
Следовательно,
Пример 17.
Найти .
.
Пусть
 ,
тогда
,
тогда ,
или
,
или .
Следовательно,
.
Следовательно,
В заключение отметим, что разные способы интегрирования одной и той же функции иногда приводят к функциям, различным по своему виду. Это кажущееся противоречие можно устранить, если показать, что разность между полученными функциями есть постоянная величина (см. теорему, доказанную на лекции 1).
Примеры:
Результаты отличаются на постоянную величину, и, значит, оба ответа верны.
б) I= .
.

Легко убедиться, что любые из ответов отличаются друг от друга только на постоянную величину.
б) Метод подстановки (метод введения новой переменной)
Пусть интеграл
 (
( - непрерывна) не может быть непосредственно
преобразован к виду табличного. Сделаем
подстановку
- непрерывна) не может быть непосредственно
преобразован к виду табличного. Сделаем
подстановку ,
где
,
где - функция, имеющая непрерывную производную.
Тогда
- функция, имеющая непрерывную производную.
Тогда ,
, и
и
 .
(3)
.
(3)
Формула (3) называется формулой замены переменной в неопределенном интеграле.
Как правильно выбрать подстановку? Это достигается практикой в интегрировании. Но можно установить ряд общих правил и некоторых приемов для частных случаев интегрирования.
Правило интегрирования способом подстановки состоит в следующем.
Определяют, к какому табличному интегралу приводится данный интеграл (предварительно преобразовав подынтегральное выражение, если нужно).
Определяют, какую часть подынтегральной функции заменить новой переменной, и записывают эту замену.
Находят дифференциалы обеих частей записи и выражают дифференциал старой переменной (или выражение, содержащее этот дифференциал) через дифференциал новой переменной.
Производят замену под интегралом.
Находят полученный интеграл.
Производят обратную замену, т.е. переходят к старой переменной.
Проиллюстрируем правило примерами.
Пример
18.
Найти .
.

Пример
19.
Найти .
.

 =
= .
.
Этот интеграл найдем подведением
 под
знак дифференциала.
под
знак дифференциала.
 =.
=.
Пример 20.
Найти (
( ).
).

 ,
т.е.
,
т.е. ,
или
,
или .
Отсюда
.
Отсюда ,
т.е.
,
т.е. .
.
Таким образом, имеем
 .
Заменяя
.
Заменяя его выражением черезx
, окончательно
находим интеграл, играющий важную роль
в интегрировании иррациональных функций:
его выражением черезx
, окончательно
находим интеграл, играющий важную роль
в интегрировании иррациональных функций: (
( ).
).
Студенты прозвали этот интеграл «длинным логарифмом».
Иногда вместо подстановки
 лучше выполнять замену переменной вида
лучше выполнять замену переменной вида .
.
Пример 21.
Найти .
.

Пример 22.
Найти .
.
Воспользуемся подстановкой
 .
Тогда
.
Тогда ,
, ,
, .
.
Следовательно, .
В ряде случаев нахождение интеграла основывается на использовании методов непосредственного интегрирования и подведения функций под знак дифференциала одновременно (см. пример 12).
Проиллюстрируем этот комбинированный подход к вычислению интеграла, играющего важную роль при интегрировании тригонометрических функций.
Пример 23.
Найти .
.

= .
.
Итак,
 .
.
Другой подход к вычислению этого интеграла:
 .
.
Пример 24.
Найти .
.
Заметим, что удачный выбор подстановки обычно представляет трудности. Для их преодоления необходимо овладеть техникой дифференцирования и хорошо знать табличные интегралы.
Функция F(x), дифференцируемая в данном промежутке X, называется первообразной для функции f(x), или интегралом от f(x), если для всякого x ∈X справедливо равенство:
F " (x) = f(x). (8.1)
Нахождение всех первообразных для данной функции называется ее интегрированием. Неопределенным интегралом функции f(x) на данном промежутке Х называется множество всех первообразных функций для функции f(x); обозначение -
Если F(x) - какая-нибудь первобразная для функции f(x), то ∫ f(x)dx = F(x) + C, (8.2)
где С- произвольная постоянная.
Таблица интегралов
Непосредственно из определения получаем основные свойства неопределенного интеграла и список табличных интегралов:
1) d∫f(x)dx=f(x)
2)∫df(x)=f(x)+C
3) ∫af(x)dx=a∫f(x)dx (a=const)
4) ∫(f(x)+g(x))dx = ∫f(x)dx+∫g(x)dx
Список табличных интегралов
1. ∫x m dx = x m+1 /(m + 1) +C; (m ≠ -1)
3.∫a x dx = a x /ln a + C (a>0, a ≠1)
4.∫e x dx = e x + C
5.∫sin x dx = cosx + C
6.∫cos x dx = - sin x + C
7. = arctg x + C
8. = arcsin x + C
10. = - ctg x + C
Замена переменной
Для интегрирования многих функций применяют метод замены переменной или подстановки, позволяющий приводить интегралы к табличной форме.
Если функция f(z) непрерывна на [α,β], функция z =g(x) имеет на непрерывную производную и α ≤ g(x) ≤ β, то
∫ f(g(x)) g " (x) dx = ∫f(z)dz, (8.3)
причем после интегрирования в правой части следует сделать подстановку z=g(x).
Для доказательства достаточно записать исходный интеграл в виде:
∫ f(g(x)) g " (x) dx = ∫ f(g(x)) dg(x).
Например:
Метод интегрирования по частям
Пусть u = f(x) и v = g(x) - функции, имеющие непрерывные . Тогда, по произведения,
d(uv))= udv + vdu или udv = d(uv) - vdu.
Для выражения d(uv) первообразной, очевидно, будет uv, поэтому имеет место формула:
∫ udv = uv - ∫ vdu (8.4.)
Эта формула выражает правило интегрирования по частям . Оно приводит интегрирование выражения udv=uv"dx к интегрированию выражения vdu=vu"dx.
Пусть, например, требуется найти ∫xcosx dx. Положим u = x, dv = cosxdx, так что du=dx, v=sinx. Тогда
∫xcosxdx = ∫x d(sin x) = x sin x - ∫sin x dx = x sin x + cosx + C.
Правило интегрирования по частям имеет более ограниченную область применения, чем замена переменной. Но есть целые классы интегралов, например,
∫x k ln m xdx, ∫x k sinbxdx, ∫ x k cosbxdx, ∫x k e ax и другие, которые вычисляются именно с помощью интегрирования по частям.
Определенный интеграл
Понятие определенного интеграла вводится следующим образом. Пусть на отрезке определена функция f(x). Разобьем отрезок [
a,b] на n
частей точками a= x 0 < x 1 <...< x n = b. Из каждого интервала (x i-1 ,
x i) возьмем произвольную точку ξ i и составим сумму f(ξ i)
Δx i где
Δ
x i =x i - x i-1
. Сумма вида f(ξ i)Δ
x i называется интегральной суммой
, а ее предел при λ = maxΔx i → 0, если он существует и конечен, называется определенным интегралом
функции f(x) от a
до b
и обозначается:
F(ξ i)Δx i (8.5).
Функция f(x) в этом случае называется интегрируемой на отрезке , числа a и b носят название нижнего и верхнего предела интеграла .
Для определенного интеграла справедливы следующие свойства:
4), (k = const, k∈R);
5)![]()
6)![]()
7) f(ξ)(b-a) (ξ∈).
Последнее свойство называется теоремой о среднем значении .
Пусть f(x) непрерывна на . Тогда на этом отрезке существует неопределенный интеграл
∫f(x)dx = F(x) + C
и имеет место формула Ньютона-Лейбница , cвязывающая определенный интеграл с неопределенным:
F(b) - F(a). (8.6)
Геометрическая интерпретация: определенный интеграл представляет собой площадь криволинейной трапеции, ограниченной сверху кривой y=f(x), прямыми x = a и x = b и отрезком оси Ox .
Несобственные интегралы
Интегралы с бесконечными пределами и интегралы от разрывных (неограниченных) функций называются несобственными. Несобственные интегралы I рода - это интегралы на бесконечном промежутке, определяемые следующим образом:
![]() (8.7)
(8.7)
Если этот предел существует и конечен, то называется сходящимся несобственным интегралом от f(x) на интервале [а,+ ∞), а функцию f(x) называют интегрируемой на бесконечном промежутке [а,+ ∞). В противном случае про интеграл говорят, что он не существует или расходится .
Аналогично определяются несобственные интегралы на интервалах (-∞,b] и (-∞, + ∞):
Определим понятие интеграла от неограниченной функции. Если f(x) непрерывна для всех значений x отрезка , кроме точки с, в которой f(x) имеет бесконечный разрыв, то несобственным интегралом II рода от f(x) в пределах от a до b называется сумма:
![]()
если эти пределы существуют и конечны. Обозначение:
Примеры вычисления интегралов
Пример 3.30. Вычислить ∫dx/(x+2).
Решение. Обозначим t = x+2, тогда dx = dt, ∫dx/(x+2) = ∫dt/t = ln|t| + C = ln|x+2| + C .
Пример 3.31 . Найти ∫ tgxdx.
Решение. ∫ tgxdx = ∫sinx/cosxdx = - ∫dcosx/cosx. Пусть t=cosx, тогда ∫ tgxdx = -∫ dt/t = - ln|t| + C = -ln|cosx|+C.
Пример 3.32 . Найти ∫dx/sinxРешение.
Пример 3.33. Найти .
Решение. = .
Пример 3.34 . Найти ∫arctgxdx.
Решение. Интегрируем по частям. Обозначим u=arctgx, dv=dx. Тогда
du = dx/(x 2 +1), v=x, откуда ∫arctgxdx = xarctgx - ∫ xdx/(x 2 +1) = xarctgx + 1/2 ln(x 2 +1) +C; так как
∫xdx/(x 2 +1) = 1/2 ∫d(x 2 +1)/(x 2 +1) = 1/2 ln(x 2 +1) +C.
Пример 3.35 . Вычислить ∫lnxdx.
Решение.
Применяя формулу интегрирования по частям, получим:
u=lnx, dv=dx, du=1/x dx, v=x. Тогда ∫lnxdx = xlnx - ∫x 1/x dx =
= xlnx - ∫dx + C= xlnx - x + C.
Пример 3.36 . Вычислить ∫e x sinxdx.
Решение.
Обозначим u = e x , dv = sinxdx, тогда du = e x dx, v =∫sinxdx= - cosx → ∫ e x sinxdx = - e x cosx + ∫ e x cosxdx. Интеграл
∫e x cosxdx также интегрируем по частям: u = e x , dv = cosxdx,
du=e x dx, v=sinx. Имеем:
∫ e x cosxdx = e x sinx - ∫ e x sinxdx. Получили соотношение
∫e x sinxdx = - e x cosx + e x sinx - ∫ e x sinxdx, откуда 2∫e x sinx
dx = - e x cosx + e x sinx + С.
Пример 3.37. Вычислить J = ∫cos(lnx)dx/x.
Решение. Так как dx/x = dlnx, то J= ∫cos(lnx)d(lnx). Заменяя lnx через t, приходим к табличному интегралу J = ∫ costdt = sint + C = sin(lnx) + C.
Пример 3.38 . Вычислить J = .
Решение.
Учитывая, что = d(lnx), производим подстановку lnx = t. Тогда J = ![]() .
.
Пример
3.39
. Вычислить интеграл J = ![]() .
.
Решение.
Имеем: ![]() . Поэтому =
. Поэтому =
=
=.
вводится так sqrt(tan(x/2)).
А если в окне результата нажмете на Show steps в правом верхнем углу, то получите подробное решение.